在行测试题之中,判断推理之逻辑判断的翻译推理是一个题型特征较为明显而技巧性又较足的模块。在考试中对于考生来说,基本都能在看到题目中的一些典型逻辑关联词语时快速判定好题型。当然,在一些难题偏题中也会出现一些不太常规的替代关联词,就需要考生打好坚实的基础,从根源上理解翻译推理的核心理论,掌握推理技巧。

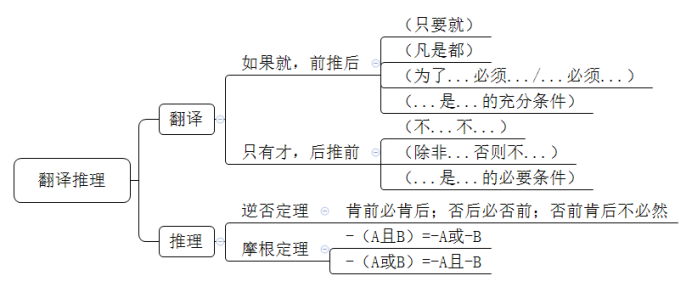
其实,简单来理解的话,翻译推理类的题型需要考生掌握的,一方面是学会将各类逻辑关联词翻译成推出关系的逻辑表达式;另一方面就是在翻译完成之后学会用符合推理规则的对选项做出判断。因此,总结来说,我们既要掌握好翻译方法,也要掌握一系列推理规则。那么,在这里就帮助大家将逻辑判断中的一些翻译推理知识点做出梳理:
翻译
“如果就,前推后”
首先,这里的“如果就”,并不仅仅是一个逻辑关联词语。它指代的是一类翻译,即充分条件假言命题的翻译。那么,当题干中出现了“如果...就...”、“如果...那么...”这样的关联词时,我们就要有足够的敏感性,是可以翻译的。具体如何翻译呢,我们通过这句话来理解下:“如果你是湖北人,那么你是中国人”;也就是“湖北人→中国人”。是不是发现,“如果就”这样的句式,是可以翻译为“前推后”这样的推出关系的。“前”即原文前半句,“后”即原文后半句。当然,我们说这是一类翻译,因此会有一系列逻辑关联词是替代“如果就”的:
“只要...就...”“倘若...则...”“凡是...都...”“要想...就...”“为了...必须...”“...必须...”“...是...的充分条件”等。
“只有才,后推前”
同样的,第二类翻译我们用“只有才”来指代,即必要条件假言命题的翻译。也就是说,当题干出现“只有..才...”这样的关联词语时,也是可以翻译的。我们通过这样一句话来理解:“只有通过笔试,才能考上公务员”;也就是“考上→通过笔试”。由于通过笔试是不一定能推出考上公务员,而考上公务员能推出通过笔试的;总结发现“只有才”这样的句式,可以翻译为“后推前”的推出关系。“前”即原文前半句,“后”即原文后半句。同样既然是一类翻译,也会有其他逻辑关联词是替代“只有才”的:
“不...不...”“除非...否则不”“...是...基础/关键/保障”“...是...必不可少/必要条件”等。
“且”命题
第三种翻译,区别在于不再是能翻译成推出关系的逻辑关联词了,而是一种命题:“且”命题(联言命题)。在学习这个命题的过程中,翻译不是难点,核心是需要我们理解命题的逻辑含义及命题的真假值:A且B,即A和B“同时成立”。因此,“A且B”只有在A、B同时成立时才为真;A、B中有一个不成立则为假。
口诀:“全真为真,一假即假”。
“或”命题
第四种翻译,同样需要重点掌握命题的逻辑含义及真假值:“或”命题(选言命题)。A或B,即A和B中“至少一个成立”。因此,“A或B”,A、B中有一个成立即为真,同时都不成立才为假。
口诀:“一真即真,全假为假”。
那么简单总结一下,我们的翻译就主要集中于这四类:
推理
了解了翻译规则,我们只是完成了第一步,将题干做出了翻译。接下来,还需要掌握重要的推理规则,对选项做出分析。而核心的两个推理规则如下:
逆否定理
前面提到,我们通过翻译可以将题干翻译成推出关系:A→B。那么,题干条件成立,即这个推出关系成立。而推出关系成立的逻辑即:A成立,则B一定成立。也就是:肯前必肯后。在此前提下,逆否定理的核心即:否后必否前。
口诀:“肯前必肯后;否后必否前;否前肯后不必然。”
摩根定理
摩根定理的核心是针对且命题及或命题,关于如何去否定这两个命题可以从命题的逻辑含义来理解。否定“A且B”,即让它不成立:A不成立或B不成立。否定“A或B”,即让它不成立:A和B都不成立。
公式:-(A且B)=-A或-B。-(A或B)=-A且-B。
观察发现,否定这样两个命题的过程,其实是发生了“且”“或”互换的。因此,我们也将之总结为“且或互换定理”:
快速记忆口诀:“负号进,且变或,或变且。”
综上,这四类翻译、两种推理是翻译推理中的基础知识点,也是必备知识点。只有充分理解了这些基础知识的逻辑核心,才能熟练运用、快速解题。因此我们在此为大家简单汇总: